Comprovamos os cossenos diretores de uma força

OBJETIVO DA EXPERIÊNCIA

Medir os ângulos que formam f com cada um dos seus componentes e calcular os seus suplementos para assim comprovar a equação dos cossenos diretores.

MATERIAIS NECESSÁRIOS

• Anilla
• Base suporte
• Círculo graduado
• Dinamómetro de 1 N
• Dinamómetro de 5 N
• Eixo tambor
• Jogo de pesos
• Nivel
• Noz dupla (5)
• Roldana com haste (2)
• Portapesos (2)
• Rodillo de 200 g
• Parafuso de mesa (2)
• Vareta suporte (2)
• Vareta suporte de 250 mm (2)
• Vareta suporte roscada

FUNDAMENTOS TEÓRICOS

Uma força 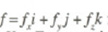forma os ângulos 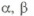, e com os eixos  X Yy Z, respetivamente, verificando-se

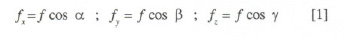
que

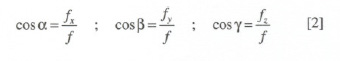
Elevando ao quadrado as igualdades anteriores, somando-as uma a uma e tendo em conta que

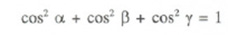
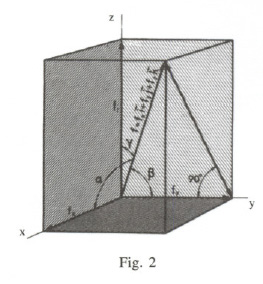
Seja uma força 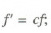 o valor das suas componentes será 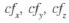(fig. 2).

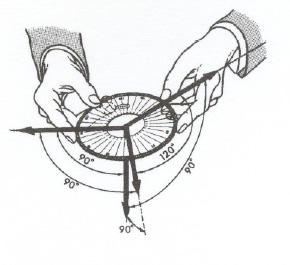
Ao substituir na [2], vê-se que resultam os mesmos ângulos 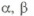e quer dizer que entre uma direção de uma força no espaço e estes ângulos que os determinam há uma correspondência biunívoca.

INSTRUÇÕES PARA REALIZAR A EXPERIÊNCIA

1. Realizar a montagem da figura 1.

2. Decompor a força devida ao rolo. Como se indicou na experiência anterior.

3. Anotar os valores obtidos de f, fx, fy, fz.

4. Medir com o círculo graduado os ângulos que forma f com cada uma das suas componentes.

5. Calcular os suplementos dos ângulos obtidos no ponto 4. Faz-se desta forma, porque as fx, fy, fz não são realmente as componentes de f, mas sim as componentes da sua oposta, onde se equilibra, ou seja, a reação.

6. Calcular os cósenos dos ângulos obtidos no ponto anterior, por meio das tabelas trigonométricas.

7. Comprovar a equação [3] e ao mesmo tempo o valor dos ângulos a, J3y y (Fig. 3).

8. Calcular os cossenos directores a partir das equações [2] com os resultados obtidos no ponto 3.

9. Comprovar aplicando a fórmula [3].

10. Calcular o arco dos cossenos obtidos no ponto 8.

11. Comparar os resultados dos pontos 4. e 10. As divergencias são os erros experimentais. O resultado das medidas efetuadas de uma ou outra obtém-se com as operações 7. e 9.

Para comprovar que 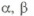é uma invariante para todas as forças que têm a mesma direção de f, faz-se da seguinte forma. Substitui-se o rolo por um dinamómetro (Fig. 1), força-se até que marque 120 g e voltam a repetir-se as operações do ponto anterior para calcular as componentes fx, fy fz, e os ângulos .

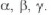Uma vez feito isto, voltar a forçar o dinamómetro para que marque 240 g, ou seja, o dobro; fazer a decomposição da força nas suas componentes e medir os ângulos correspondentes observar-se-á:

Que as componentes são o dobro das fx, fy fz, determinadas anteriormente, e que os ângulos não terão variado, sempre que a anilha esteja no mesmo ponto.

SUGESTÕES

. Baixar a noz que segura o rolo até que a força f fique horizontal. Que componente fica nula?

• Variar a posição da colocação da vareta, sendo f a mesma. Mantêm-se fx, fy, fz?

VIDEO DA EXPERIÊNCIA